数据结构排序

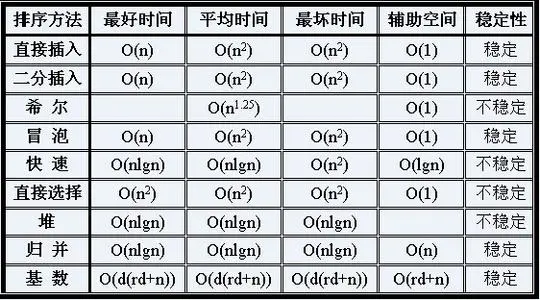
插入排序

直接插入排序

把待排序的数据插入到已经排好序的数据中，直到所有的数据插入完成.
例子：

希尔排序

希尔排序就是在前面直接插入排序的基础上进行改进的一种排序。直接插入排序的变量 i 其实就是一个间隔，而希尔排序的间隔不是 1，它的间隔逐渐缩小直到为 1 的一种排序，因此又叫缩小增量法。它是对直接插入排序算法的优化，当间隔不为 1 的时候，都是预排序。第一次的间隔是 数据长度的三分之一再加一。即 gap = size / 3 + 1（间隔几个进行比较，）
例子：

选择排序

直接选择排序

直接选择排序就是在待排序的数据中选择一个最大的或者最小的放在带待排序数据的末尾
例子：

交换排序

冒泡排序

从第一个数开始，和第二个数比较，满足条件就进行交换，然后第二个数和第三个数进行比较满足进行交换，直到最后一个数，这是一个“泡”已经冒出。现在有从开始比较，这个时候总的比较的数减少一个，因为“泡”已经冒出了。冒泡排序一共会进行 size - 1次冒泡，每次的比较次数为size - i，i是比较的第几次。
例子：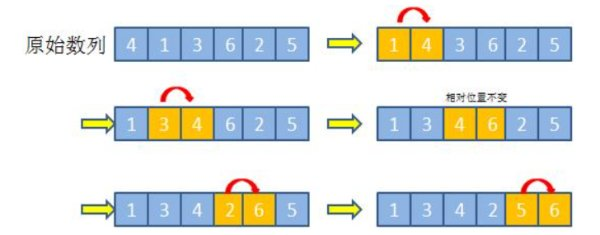

java代码实现：

public class demo_sort {
    public static void main(String[] args) {
        //冒泡排序算法
        int[] numbers=new int[]{1,5,8,2,3,9,4};
        //需进行length-1次冒泡
        for(int i=0;i<numbers.length-1;i++)
        {
            for(int j=0;j<numbers.length-1-i;j++)
            {
                if(numbers[j]>numbers[j+1])
                {
                    int temp=numbers[j];
                    numbers[j]=numbers[j+1];
                    numbers[j+1]=temp;
                }
            }
        }
        System.out.println("从小到大排序后的结果是:");
        for(int i=0;i<numbers.length;i++)
            System.out.print(numbers[i]+" ");
    }
}

快速排序

快速排序：

1. 选择一个基准元素,通常选择第一个元素或者最后一个元素,
2. 通过一趟排序讲待排序的记录分割成独立的两部分，其中一部分记录的元素值均比基准元素值小。另一部分记录的 元素值比基准值大。
3. 此时基准元素在其排好序后的正确位置
4. 然后分别对这两部分记录用同样的方法继续进行排序，直到整个序列有序
   例子：
   
   以上完成第一次比较，左右两边还要进行比较
   java代码实现：

   public static void quickSort(int[] arr){
       qsort(arr, 0, arr.length-1);
   }
   private static void qsort(int[] arr, int low, int high){
       if (low < high){
           int pivot=partition(arr, low, high);        //将数组分为两部分
           qsort(arr, low, pivot-1);                   //递归排序左子数组
           qsort(arr, pivot+1, high);                  //递归排序右子数组
       }
   }
   private static int partition(int[] arr, int low, int high){
       int pivot = arr[low];     //枢轴记录
       while (low<high){
           while (low<high && arr[high]>=pivot) --high;
           arr[low]=arr[high];             //交换比枢轴小的记录到左端
           while (low<high && arr[low]<=pivot) ++low;
           arr[high] = arr[low];           //交换比枢轴小的记录到右端
       }
       //扫描完成，枢轴到位
       arr[low] = pivot;
       //返回的是枢轴的位置
       return low;
   }